Пакет matplotlib. Наводим красивости

Продолжаем разговор о пакете matplotlib. Сегодня обсудим способы изменения внешнего вида элементов диаграмм - другими словами способы наведения красивостей.

Изменение свойств графических элементов пакета matplotlib

Как уже неоднократно отмечалось - в логике matplotlib каждый графический элемент (линия, подпись, рамка, сетка и т.д.) представлен объектом соответствующего класса. Команды (функции) пакета matplotlib, отвечающие за создание какого-либо элемента, как результат выполнения возвращают ссылку на объект представляющий данный элемент:

>>> import matplotlib.pyplot as plt
>>> line, = plt.plot([1, 2, 3])
>>> line
<matplotlib.lines.Line2D object at 0x030509D0>
>>> type(line)
<class 'matplotlib.lines.Line2D'>
>>> caption = plt.title(u'Заголовок диаграммы')
>>> caption
<matplotlib.text.Text object at 0x0308FC90>
>>> type(caption)
<class 'matplotlib.text.Text'>

Авторы пакета matplotlib предусмотрели три способа изменения свойств графических объектов.

Первый способ. Каждая команда пакета, создающая тот или иной графический элемент, принимает набор именованных переменных (для каждой из этих переменных уже задано значение по умолчанию), имена которых, как правило, совпадают с именами соответствующих полей (свойств) объекта. Изменяя значения именованных переменных можно изменять свойства создаваемого объекта:

>>> plt.plot([1, 2, 3], color = 'red', marker = '^', linestyle = '--', linewidth = 2, markersize = 5, label = u'Прямая линия')
[<matplotlib.lines.Line2D object at 0x02E3E150>]
>>> plt.title(u'Заголовок диаграммы', color = 'black', family = 'fantasy', fontsize = 'x-large')
<matplotlib.text.Text object at 0x02E66E10>

Второй способ. Как и подобает в соответствии с догмами объектно-ориентированного программирования, для каждого поля объекта существуют методы, предоставляющие возможность читать/писать значение поля. Уже существующий объект можно настроить посредством указанных методов:

>>> line, = plt.plot([1, 2, 3])
>>> line.set_color('red')
>>> line.set_marker('^')
>>> line.set_linestyle('--')
>>> line.set_linewidth(2)

В matplotlib принято следующее соглашение по именованию методов - метод возвращающий значение свойства property именуется get_property(), метод изменяющий значение свойства set_property()

Третий способ. Часто возникает необходимость для группы объектов (не обязательно экземпляров одного и того же класса) установить одинаковые значения для одного (нескольких) общих свойств. На этот случай авторы matplotlib предусмотрели специальную функцию matplotlib.pyplot.setp(*args, **kwargs) - "setup property" - установить свойство. Функция принимает ссылку или список ссылок на объекты и произвольный набор именованных переменных соответствующих изменяемым свойствам:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> X = np.linspace(0.0, 5.0, 10)
>>> Y1 = X
>>> Y2 = 3 * X
>>> Y3 = 7 * X
>>> lines = plt.plot(X, Y1, X, Y2, X, Y3)
>>> plt.setp(lines, color = 'red', marker = '^', linestyle = '--', linewidth = 2)
[None, None, None, None, None, None, None, None, None, None, None, None]
>>> plt.show()

В результате выполнения кода примера появиться вот такое окно:

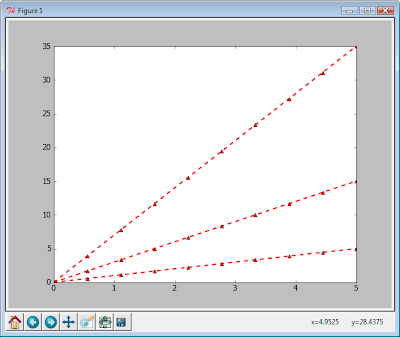
Все три линии на диаграмме оформлены одинаково.

А какой глубокий смысл кроется в структуре возвращаемой функцией setp() я, честно говоря, не знаю.

Возможен и альтернативный синтаксис вызова функции. Вместо набора именованных переменных функция принимает набор пар: строка - имя свойства, произвольный тип - значение свойства (так принято работать с объектами в Matlab):

>>> plt.setp(lines, 'color', 'red', 'marker', '^', 'linestyle', '--', 'linewidth', 2)

Если необходимо узнать какие значения допустимы для того или иного свойства объекта, можно вызвать функцию setp() передав ей ссылку на объект и строку - имя свойства.

>>> plt.setp(line, 'linestyle')
 linestyle: [ '-' | '--' | '-.' | ':' | 'None' | ' ' | '' ] and any drawstyle in combination with a linestyle, e.g. 'steps--'.
>>> plt.setp(line, 'color')
 color: any matplotlib color

Если вызвать функцию setp(), передав только ссылку на объект, будет выведен список всех свойств объекта и список возможных значений для каждого из свойств:

>>> plt.setp(line)
  alpha: float (0.0 transparent through 1.0 opaque)
  animated: [True | False]
  antialiased or aa: [True | False]
  axes: an :class:`~matplotlib.axes.Axes` instance
  ...

Ну и если первый аргумент функции - список ссылок на объекты, описанные выше действия производятся для объекта, ссылка на который стоит в переданном списке первой.

В качестве примера приведу код программы использующей все три способа настройки объектов.

Для начала построим диаграмму без каких либо дополнительных настроек, пусть все свойства всех объектов будут инициализированы системой значениями по умолчанию.

# -*- coding: UTF-8 -*-

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

# Значения по оси X
X = np.linspace(0.0, 2.0, 15)
# Значения по оси Y
Y_01 = X
Y_02 = X * 3
Y_03 = X * 7

# Задаем размер диаграммы
mpl.rcParams['figure.figsize'] = (8.0, 6.0)

# Строим диаграмму
# Линии
line_01 = plt.plot(X, Y_01)
line_02 = plt.plot(X, Y_02)
line_03 = plt.plot(X, Y_03)

# Сохраняем диаграмму в файл
plt.savefig('set_exmp_01.png', format = 'png')

В результате получим вот такое изображение:

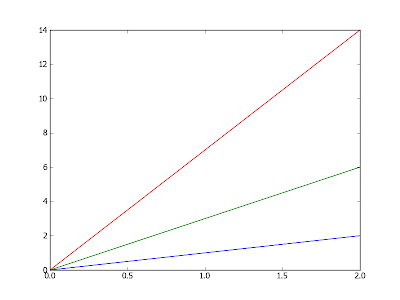
Теперь, взяв за основу код предыдущего примера, настроим, как хотим, свойства каждой прямой.

# -*- coding: UTF-8 -*-

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

# Значения по оси X
X = np.linspace(0.0, 2.0, 15)
# Значения по оси Y
Y_01 = X 
Y_02 = X * 3
Y_03 = X * 7

# Задаем размер диаграммы
mpl.rcParams['figure.figsize'] = (8.0, 6.0)

# Строим диаграмму

# Линии

# Первый способ настройки объектов
line_01, = plt.plot(X, Y_01, color = 'blue', linestyle = ':', linewidth = 1, marker = 's',  markersize = 6, markeredgecolor = 'black', markerfacecolor = 'blue', markeredgewidth = 1, label = u'y = x' )

line_02,  = plt.plot(X, Y_02)
line_03,  = plt.plot(X, Y_03)

# Второй способ настройки объектов
line_02.set_color('red')
line_02.set_linestyle(':')
line_02.set_linewidth(1)
line_02.set_marker('D')
line_02.set_markersize(5)
line_02.set_markeredgecolor('black')
line_02.set_markerfacecolor('red')
line_02.set_markeredgewidth(1)
line_02.set_label(u'y = 3 * x')

# Третьий способ настройки объектов
plt.setp(line_03, color = 'magenta', linestyle = ':', linewidth = 1, marker = 'o', markersize = 6, markeredgecolor = 'black', markerfacecolor = 'magenta', markeredgewidth = 1, label = u'y = 7 * x')

# Задаем интервалы значений по осям X, Y
plt.axis((-0.03, 2.03, -0.2, 14.2))

# Добавим легенду
plt.legend(loc = 'best')

# Сохраняем диаграмму в файл
plt.savefig('set_exmp_02.png', format = 'png')

Теперь изображение будет выглядеть вот так:

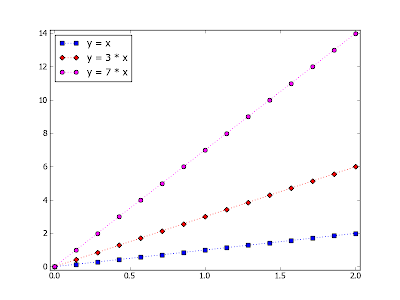
В примерах, для формирования массивов значений был использован модуль NumPy. С описанием использованных функций этого модуля можно познакомиться прочтя пост Пакет NumPy. Краткое введение

Остановимся подробнее на свойствах объектов класса matplotlib.lines.Line2D - линии, которая неизбежно присутствует практически на каждой диаграмме.

О свойствах объектов класса matplotlib.lines.Line2D

Ниже в таблице приведены основные свойства объекта класса matplotlib.lines.Line2D.

Свойство	Значение	Описание
alpha	Вещественное число в интервале [0.0, 1.0]	Степень прозрачность элементов линии (собственно линии и маркеров) - от полностью прозрачного 0.0, до полностью непрозрачного 1.0. Пример использования смотри ниже
antialiased или aa	True, False	Включить (True), выключить (False) режим антиалиазинга элементов линии
color или c	Один из возможных способов представления цвета в matplotlib, подробности смотри ниже	Цвет линии
dash_capstyle	Строки: 'butt', 'round', 'projecting'	Стиль оконечностей пунктирной линии. Пример использования смотри ниже
dash_joinstyle	Строки: 'miter', 'round', 'bevel'	Стиль соединения пунктирных линий
dashes	Список (кортеж) целых чисел, количество элементов списка должно быть четным	Каждая пара чисел в списке рассматривается как количество индуцируемых точек, количество погашенных точек. С помощью свойства dashes можно рисовать линии состоящие из произвольного повторяющегося набора штрихов и пунктиров. Пример использования смотри ниже
drawstyle	Строки: 'default', 'steps', 'steps-pre', 'steps-mid', 'steps-post'	Стиль отображения линии: 'default' - соседние точки соединены прямой, остальные значения - соседние точки соединены пересекающимися под прямым углом отрезками ("ступенькой") с различными вариациями пересечения отрезков. Пример использования смотри ниже
label	Произвольная строка	Подпись к линии, используется при создании легенды диаграммы
linestyle или ls	Строки: '-', '--', '-.', ':', 'steps', 'steps-pre', 'steps-mid', 'steps-post', 'None', ' ', ''	Стиль линии. Пример использования первых четырех стилей был приведен ранее, пример использования следующих четырех (можно задавать и через свойство drawstyle) смотри ниже, 'None', пробел и пустая строка выключают отображение линии, (собственно линии, маркеры, при этом, будут отображаться)
linewidth или lw	float	Толщина линии в точках
marker	Строки: '.', ',', 'o', 'v', '^', '<', '>', '1', '2', '3', '4', 's', 'p', '*', 'h', 'H', '+', 'x', 'D', 'd', '|', '_'	Стиль маркера. Пример использования был приведен ранее
markeredgecolor или mec	Один из возможных способов представления цвета в matplotlib, подробности смотри ниже	Цвет границы маркера
markeredgewidth или mew	float	Толщина границы маркера в точках
markerfacecolor или mfc	Один из возможных способов представления цвета в matplotlib, подробности смотри ниже	Цвет маркера
markersize или ms	float	Размер маркера в точках
markevery	None, integer N, список/кортеж (integer start, integer N)	Свойство определяет, как будут использоваться маркеры при построении данной линии. Если None будут отображены все маркеры. Если целое число N, будет отображен каждый N-ый маркер. Если кортеж целых чисел (start, N) будет отображен каждый N-ый маркер начиная с start. Пример использования смотри ниже
solid_capstyle	Строки: 'butt', 'round', 'projecting'	Стиль оконечностей непрерывной линии
solid_joinstyle	Строки: 'miter', 'round', 'bevel'	Стиль соединения непрерывных линий
visible	True, False	В случае False линия и маркеры становятся невидимыми. True включает отображение элементов линии
zorder	integer	Порядок наложения элементов диаграммы (Z-order). Элемент с наибольшим значением zorder будет отображен на переднем плане (по отношению к наблюдателю) или, другими словами, элемент с наибольшим zorder будет отображен последним (самым верхним). Пример использования смотри ниже

Способы представления цвета в пакете matplotlib

Как следует из названия подраздела цвет в matplotlib может быть задан несколькими способами.

Способ первый. Из системы Matlab позаимствованы обозначения для восьми базовых цветов в виде отдельных символов.

Символ	Цвет
'b'	blue	синий
'g'	green	зеленый
'r'	red	красный
'c'	cyan	бирюзовый
'm'	magenta	пурпурный
'y'	yellow	желтый
'k'	black	черный
'w'	white	белый

>>> plt.plot(X, Y_02, color = 'm')

Способ второй. Цвет можно задать используя стандартные обозначения цветов принятые в html, как то 'red', 'silver', 'olive' и так далее.

>>> plt.plot(X, Y_02, color = 'navy')

Способ третий. Произвольный цвет можно задать воспользовавшись HEX стилем представления цвета в html: '#cc00cc', '#9900ff', '#0099cc'.

>>> plt.plot(X, Y_02, color = '#003399')

Способ четвертый. Произвольный цвет так же можно задать передав кортеж из трех вещественных чисел, каждое из которых пренадлежит интервалу [0.0, 1.0]. Числа соответствуют представлению цвета в системе RGB: (0.75, 0.0, 1.0), (1.0, 0.33, 0.33), (0.0, 0.47, 0.21).

>>> plt.plot(X, Y_02, color = (0.0, 0.5, 0.32))

Способ пятый. Вариация на тему четвертого способа. Цвет в градации серого можно задать передав строку являющуюся представлением вещественного числа в диапазоне [0.0, 1.0], '0.0' - совсем черный, '1.0' - совсем белый.

>>> plt.plot(X, Y_02, color = '0.75')

Свойства linestyle и drawstyle

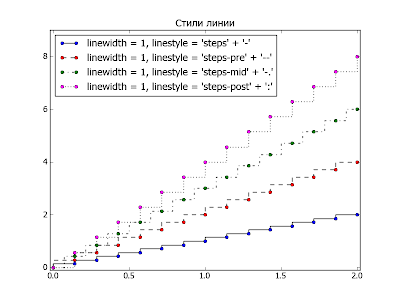
Свойство linestyle включает в себя свойство drawstyle - стили отрисовки "ступенек" можно задать как через drawstyle так и через linestyle. Пример использования на рисунке ниже:

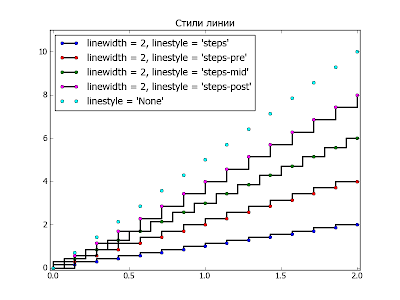
Значения свойства drawstyle и остальные значения свойства linestyle можно комбинировать. Пример на рисунке ниже:

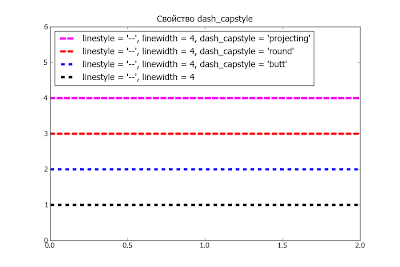
Свойство dash_capstyle

Для того, чтобы ясно углядеть различия в начертаниях "кончика штриха" необходимо установить толщину линии как минимум в четыре точки. Пример использования на рисунке:

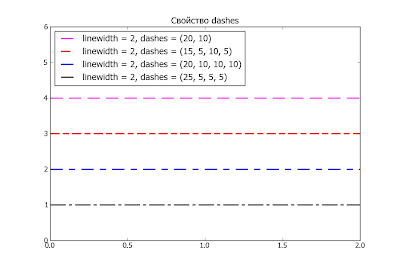
Свойство dashes

Когда существующие стили пунктирных линий не устраивают, можно поиграться с значениями свойства dashes:

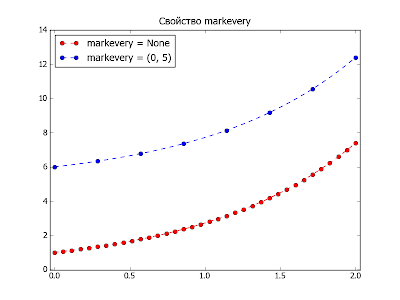
Свойство markevery

Когда данных много и при этом хочется отобразить линию с маркерами, избыточные маркеры, во избежании их слияния, необходимо как то удалить. Можно конечно специально отфильтровать данные (сделать выборку данных), но проще воспользоваться свойством markevery. Вот код примера:

# -*- coding: UTF-8 -*-

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

# Значения по оси X
X = np.linspace(0.0, 2.0, 36)
# Значения по оси Y
Y_01 = np.exp(X)
Y_02 = np.exp(X) + 5.0

# Задаем размер диаграммы
mpl.rcParams['figure.figsize'] = (8.0, 6.0)

# Строим диаграмму

# Линии
line_01,  = plt.plot(X, Y_01, 'ro--', markevery = None, label ='markevery = None')
line_02,  = plt.plot(X, Y_02, 'bo--', markevery = (0, 5), label = 'markevery = (0, 5)')
# Подпись к диаграмме
plt.title(u'Свойство markevery')
# Добавляем легенду
plt.legend(loc = 'best')
# Задаем интервалы значений по осям X, Y
plt.axis((-0.03, 2.03, -0.03, 14.0))

# Сохраняем диаграмму в файл
plt.savefig('markevery.png', format = 'png')

А вот результат прогона кода:

Свойство zorder

Чем больше значение свойства zorder тем ближе к наблюдателю объект:

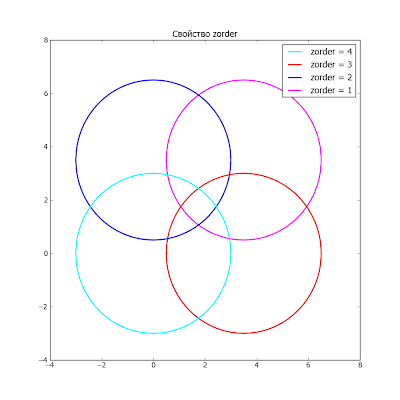
Свойство alpha

Для иллюстрации "прозрачности" воспользуемся предыдущим рисунком. Получилось коряво, но смысл свойства alpha понять можно (в matplotlib атрибут прозрачности жутко портит некоторые цвета)

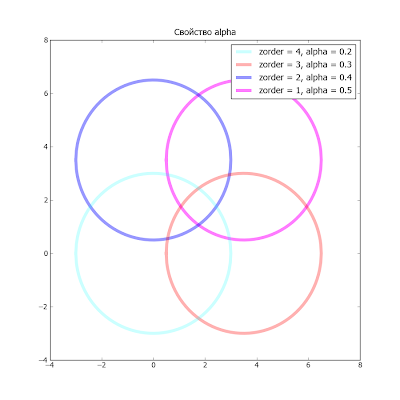
Ну вот пожалуй на сегодня и все...

Предыдущий пост по теме: Пакет matplotlib. График с дополнительной осью ординат.

Читать далее...

Подсветка синтаксиса в блоге. Используем онлайновые маркеры синтаксиса

О том, как вставить в блог фрагмент кода с подсвеченным синтаксисом, используя редактор Vim, я уже писал. А недавно мне подсказали еще более простое решение, не требующее для своей реализации ни чего кроме браузера - в сети имеются специальные (абсолютно бесплатные) сервисы, позволяющие разукрашивать, перед публикацией, практически любой код. Принцип работы с клиентом у таких сервисов-маркеров общий: пользователь вводит в форму фрагмент кода, выбирает из выпадающего списка тип оформляемого кода, включает (если нужно) пару дополнительных опций и, нажав соответствующую кнопку, отправляет запрос сервису. Сервис возвращает подсвеченный код в виде блока тегов html, который можно скопировать и вставить в свою страницу. Список поддерживаемых языков кода у сервисов весьма обширный, разукрасить можно практически все что угодно.

Вот два таких онлайновых маркера.

Online syntax highlighting

Online syntax highlighting, способен автоматически угадывать тип введенного кода, позволяет выбрать несколько стилей оформления. Вставляем код в редактор Source code, выбираем язык программирования в списке Type, стиль оформления в списке Style, жмем кнопку Highlight, в появившемся редакторе выделяем и копируем блок html тегов.

Примеры подсвеченного кода при различных стилях оформления:

Стиль: white

# -*- coding: UTF-8 -*-

import matplotlib.pyplot as plt

# Значения по оси X
X = [20.0, 40.0, 60.0, 80.0, 100.0]
# Набор значений по оси Y
Y_10 = [0.97252, 0.94238, 0.89927, 0.85197, 0.79784]
Y_20 = [0.96864, 0.93518, 0.89113, 0.84344, 0.78934]
Y_30 = [0.96395, 0.92770, 0.88278, 0.83473, 0.78075]

# Строим диаграмму
plt.plot(X, Y_10, 'bD:',  label = u'Температура 10 \u00b0C')
plt.plot(X, Y_20, 'r^:',  label = u'Температура 20 \u00b0C')
plt.plot(X, Y_30, 'go:',  label = u'Температура 30 \u00b0C')
# Задаем подписи
plt.title(u'Зависимость плотности водных растворов этилового спирта от температуры')
plt.xlabel(u'Массовая доля этилового спирта, %')
plt.ylabel(u'Плотность, г/мл')
# Включаем легенду
plt.legend(loc = 'best')
# Сохраняем построенную диаграмму в файл
plt.savefig('spirit.png', format = 'png')

Стиль: navy

# -*- coding: UTF-8 -*-

import matplotlib.pyplot as plt

# Значения по оси X
X = [20.0, 40.0, 60.0, 80.0, 100.0]
# Набор значений по оси Y
Y_10 = [0.97252, 0.94238, 0.89927, 0.85197, 0.79784]
Y_20 = [0.96864, 0.93518, 0.89113, 0.84344, 0.78934]
Y_30 = [0.96395, 0.92770, 0.88278, 0.83473, 0.78075]

# Строим диаграмму
plt.plot(X, Y_10, 'bD:',  label = u'Температура 10 \u00b0C')
plt.plot(X, Y_20, 'r^:',  label = u'Температура 20 \u00b0C')
plt.plot(X, Y_30, 'go:',  label = u'Температура 30 \u00b0C')
# Задаем подписи
plt.title(u'Зависимость плотности водных растворов этилового спирта от температуры')
plt.xlabel(u'Массовая доля этилового спирта, %')
plt.ylabel(u'Плотность, г/мл')
# Включаем легенду
plt.legend(loc = 'best')
# Сохраняем построенную диаграмму в файл
plt.savefig('spirit.png', format = 'png')

Стиль: Bred3

# -*- coding: UTF-8 -*-

import matplotlib.pyplot as plt

# Значения по оси X
X = [20.0, 40.0, 60.0, 80.0, 100.0]
# Набор значений по оси Y
Y_10 = [0.97252, 0.94238, 0.89927, 0.85197, 0.79784]
Y_20 = [0.96864, 0.93518, 0.89113, 0.84344, 0.78934]
Y_30 = [0.96395, 0.92770, 0.88278, 0.83473, 0.78075]

# Строим диаграмму
plt.plot(X, Y_10, 'bD:',  label = u'Температура 10 \u00b0C')
plt.plot(X, Y_20, 'r^:',  label = u'Температура 20 \u00b0C')
plt.plot(X, Y_30, 'go:',  label = u'Температура 30 \u00b0C')
# Задаем подписи
plt.title(u'Зависимость плотности водных растворов этилового спирта от температуры')
plt.xlabel(u'Массовая доля этилового спирта, %')
plt.ylabel(u'Плотность, г/мл')
# Включаем легенду
plt.legend(loc = 'best')
# Сохраняем построенную диаграмму в файл
plt.savefig('spirit.png', format = 'png')

Стиль: black

# -*- coding: UTF-8 -*-

import matplotlib.pyplot as plt

# Значения по оси X
X = [20.0, 40.0, 60.0, 80.0, 100.0]
# Набор значений по оси Y
Y_10 = [0.97252, 0.94238, 0.89927, 0.85197, 0.79784]
Y_20 = [0.96864, 0.93518, 0.89113, 0.84344, 0.78934]
Y_30 = [0.96395, 0.92770, 0.88278, 0.83473, 0.78075]

# Строим диаграмму
plt.plot(X, Y_10, 'bD:',  label = u'Температура 10 \u00b0C')
plt.plot(X, Y_20, 'r^:',  label = u'Температура 20 \u00b0C')
plt.plot(X, Y_30, 'go:',  label = u'Температура 30 \u00b0C')
# Задаем подписи
plt.title(u'Зависимость плотности водных растворов этилового спирта от температуры')
plt.xlabel(u'Массовая доля этилового спирта, %')
plt.ylabel(u'Плотность, г/мл')
# Включаем легенду
plt.legend(loc = 'best')
# Сохраняем построенную диаграмму в файл
plt.savefig('spirit.png', format = 'png')

Во всех примерах использован код из поста Пакет matplotlib. Строим банальный график

Syntax Highlighter

В целом порядок работы с сервисом Syntax Highlighter аналогичен описанному выше. Имеются опции: Line numbers - включить/выключить автоматическую нумерацию строк кода, Use <font> tag (for Habrahabr) - если включена, код оформляется посредством тега <font>, в противном случае с помощью классов css (внешний вид подсвеченного кода при этом несколько отличается).

Примеры:

При включенной опции Use <font> tag (for Habrahabr):

# -*- coding: UTF-8 -*-
 
import matplotlib.pyplot as plt
 
# Значения по оси X
X = [20.0, 40.0, 60.0, 80.0, 100.0]
# Набор значений по оси Y
Y_10 = [0.97252, 0.94238, 0.89927, 0.85197, 0.79784]
Y_20 = [0.96864, 0.93518, 0.89113, 0.84344, 0.78934]
Y_30 = [0.96395, 0.92770, 0.88278, 0.83473, 0.78075]
 
# Строим диаграмму
plt.plot(X, Y_10, 'bD:',  label = u'Температура 10 \u00b0C')
plt.plot(X, Y_20, 'r^:',  label = u'Температура 20 \u00b0C')
plt.plot(X, Y_30, 'go:',  label = u'Температура 30 \u00b0C')
# Задаем подписи
plt.title(u'Зависимость плотности водных растворов этилового спирта от температуры')
plt.xlabel(u'Массовая доля этилового спирта, %')
plt.ylabel(u'Плотность, г/мл')
# Включаем легенду
plt.legend(loc = 'best')
# Сохраняем построенную диаграмму в файл
plt.savefig('spirit.png', format = 'png')

При выключенной опции Use <font> tag (for Habrahabr):

# -*- coding: UTF-8 -*-
 
import matplotlib.pyplot as plt
 
# Значения по оси X
X = [20.0, 40.0, 60.0, 80.0, 100.0]
# Набор значений по оси Y
Y_10 = [0.97252, 0.94238, 0.89927, 0.85197, 0.79784]
Y_20 = [0.96864, 0.93518, 0.89113, 0.84344, 0.78934]
Y_30 = [0.96395, 0.92770, 0.88278, 0.83473, 0.78075]
 
# Строим диаграмму
plt.plot(X, Y_10, 'bD:',  label = u'Температура 10 \u00b0C')
plt.plot(X, Y_20, 'r^:',  label = u'Температура 20 \u00b0C')
plt.plot(X, Y_30, 'go:',  label = u'Температура 30 \u00b0C')
# Задаем подписи
plt.title(u'Зависимость плотности водных растворов этилового спирта от температуры')
plt.xlabel(u'Массовая доля этилового спирта, %')
plt.ylabel(u'Плотность, г/мл')
# Включаем легенду
plt.legend(loc = 'best')
# Сохраняем построенную диаграмму в файл
plt.savefig('spirit.png', format = 'png')

Ну вот на этом и все. Спасибо за внимание.

Предыдущий пост по теме: Как вставить в блог фрагмент кода с подсветкой синтаксиса

Читать далее...

Пакет NumPy. Краткое введение

Введение. Пакет NumPy - зачем нужен, где взять

Пакет (библиотека) языка Pyton NumPy предоставляет программисту средства для высокоэффективной работы с огромными многомерными массивами данных. Как составная часть и основа, пакет NumPy входит в большинство проектов, использующих язык Python и требующих мало-мальски громоздких вычислений. В частности, с его использованием написаны популярные пакеты вычислительной математики и научной графики SciPy и mathplotLib.

Python интерпретируемый язык программирования, как следствие, математические алгоритмы, написанные на Python'е, часто работают заметно медленнее по сравнению с теми же алгоритмами, реализованными на компилируемых языках. Авторы NumPy постарались разрешить эту проблему в части обработки массивов, предложив модуль, включающий набор функций для создания многомерных массивов и работы с ними, причем исполняемый код функций реализован на языках C и Fortran. Кроме того, в пакете определены функции линейной алгебры, преобразования Фурье и генерации случайных чисел.

Сейчас я постараюсь дать самое краткое описание основ использования пакета.

Взять дистрибутив NumPy можно из репозитория SourceForge. На момент написания крайняя версия 1.3.0, выпущена 05 апреля 2009 года. Установка пакета не должна вызвать каких-либо затруднений, какой-либо особой настройки пакет так же не требует.

Модуль NumPy предназначен для работы с массивами, соответственно основной тип данных определенных в модуле - массив (nump.ndarray). Массив - контейнер, содержащий элементы одного типа (и одной длинны, если элементы вложенные массивы), организованные в упорядоченную многомерную таблицу. Доступ к элементам осуществляется по индексу - кортежу целых чисел.

Создать массив можно несколькими способами.

Способы создания массивов

Массив может быть создан на основе имеющегося списка:

>>> import numpy as np

>>> a = np.array([.1, .2, .3, .4, .5])
>>> a
array([ 0.1,  0.2,  0.3,  0.4,  0.5])
>>> type(a)
<type 'numpy.ndarray'>

Имя класса numpy.ndarray выбрано специально, чтобы не было путаницы со стандартным классом Python array.

Аналогично можно создать многомерный массив:

>>> a3 = np.array([ [ [1, 2], [3, 4], [5, 6] ], [ [7, 8], [9, 10], [11, 12] ] ])
>>> a3
array([[[ 1,  2],
        [ 3,  4],
        [ 5,  6]],

       [[ 7,  8],
        [ 9, 10],
        [11, 12]]])
>>> type(a3)
<type 'numpy.ndarray'>

Массивы NumPy во многом аналогичны стандартным спискам Python.

Доступ к элементам массива получают по индексу (разумеется, индекс первого элемента 0):

>>>print a[0]
0.1

>>>print a[3]
0.4

Для индексации многомерных массивов используют кортежи (индексы перечисляют через запятую):

>>> a3[1]
array([[ 7,  8],
       [ 9, 10],
       [11, 12]])

>>> a3[1, 1]
array([ 9, 10])

>>> a3[1, 1, 1]
10

От массивов можно брать срезы:

>>> a[2:4]
array([ 0.3,  0.4])

>>> a3[0, 1:]
array([[3, 4],
       [5, 6]])

Массивы можно использовать в различных итерациях:

>>> for i in a:
...     print i
...
0.1
0.2
0.3
0.4
0.5

>>> for i in a3:
...     for j in i:
...             print j
...
[1 2]
[3 4]
[5 6]
[7 8]
[ 9 10]
[11 12]

Каждый объект numpy.ndarray имеет атрибут shape - кортеж целых чисел, который определяет шаблон массива. Здесь под шаблоном подразумевается количество элементов каждой размерности массива, так для матрицы с n строк и m столбцов шаблон (n, m).

>>> a.shape
(5,)

>>> a3.shape
(2, 3, 2)

Изменяя атрибут shape, можно изменять размерность и структуру массива, но при этом число элементов массива должно оставаться неизменным:

>>> a3.shape = (6, 2)
>>> a3
array([[ 1,  2],
       [ 3,  4],
       [ 5,  6],
       [ 7,  8],
       [ 9, 10],
       [11, 12]])

>>> a3.shape = (12)
>>> a3
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

>>> a3.shape = (3, 3)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: total size of new array must be unchanged

Массив может быть создан с помощью функции numpy.arange().

Функция arange() в самом простом варианте вызова принимает в качестве аргумента целое положительное число n, возвращает массив из n элементов от 0 до n-1:

>>> b = np.arange(5)
>>> b
array([0, 1, 2, 3, 4])
>>> type(b)
<type 'numpy.ndarray'>

Полный формат вызова функции: numpy.arange([start,] stop[, step,], dtype = None),

где:

start - опциональный аргумент, начальное значение интервала, по умолчанию равен 0;

stop - обязательный аргумент, конечное значение интервала, не входящее в сам интервал, интервал замыкает значение stop - step;

step - опциональный аргумент, шаг итерации, разность между каждым последующим и предыдущим значениями интервала, по умолчанию равен 1;

dtype - тип элементов массива, по умолчанию None, в этом случае тип элементов определяется по типу переданных функции аргуметов start, stop.

Массив может быть создан с помощью функции numpy.linspace().

Функция linspace() в простейшем случае принимает три аргумента - числа: начальный элемент массива, конечный элемент массива, количество элементов массива. Возвращает массив чисел равномерно распределенных от начального до конечного значения.

>>> c = np.linspace(-3.0, 3.0, 7)
>>> c
array([-3., -2., -1.,  0.,  1.,  2.,  3.])
>>> type(c)
<type 'numpy.ndarray'>

Полный формат вызова функции: numpy.linspace(start, stop, num = 50, endpoint = True, retstep = False),

где:

start - обязательный аргумент, первый член последовательности элементов массива;

stop - обязательный аргумент, последний член последовательности элементов массива;

num - опциональный аргумент, количество элементов массива, по умолчанию равен 50;

endpoint - опциональный аргумент, логическое значение, по умолчанию True. Если передано True, stop, последний элемент массива. Если установлено в False, последовательность элементов формируется от start до stop для num + 1 элементов, при этом в возвращаемый массив последний элемент не входит;

>>> d = np.linspace(1.0, 6.0, 5, endpoint = False)
>>> d
array([ 1.,  2.,  3.,  4.,  5.])

retstep - опциональный аргумент, логическое значение, по умолчанию False. Если передано True, функция возвращает кортеж из двух членов, первый - массив, последовательность элементов, второй - число, приращение между элементами последовательности.

>>> f = np.linspace(.5, -.5, 5, retstep = True)
>>> f
(array([ 0.5 ,  0.25,  0.  , -0.25, -0.5 ]), -0.25)

Массив может быть создан с помощью функций numpy.zeros(), numpy.ones(), numpy.empty().

Функции принимают один обязательный аргумент - кортеж, размерность массива и возвращают массив затребованной структуры содержащий: нули (функция numpy.zeros()), единицы numpy.ones(), произвольный мусор (неинициализированный массив, функция numpy.empty()):

>>> z = np.zeros((3,3))
>>> z
array([[ 0.,  0.,  0.],
       [ 0.,  0.,  0.],
       [ 0.,  0.,  0.]])

>>> o = np.ones((3, 3))
>>> o
array([[ 1.,  1.,  1.],
       [ 1.,  1.,  1.],
       [ 1.,  1.,  1.]])

>>> e = np.empty((3,3))
>>> e
array([[  8.32475314e-306,   8.32468797e-306,   8.32462278e-306],
       [  8.32455759e-306,   8.32449240e-306,   5.99491582e+197],
       [  5.30481132e+180,   5.51965256e-311,   0.00000000e+000]])

Полный формат вызова функций:

numpy.zeros(shape, dtype = float, order = 'C')

numpy.ones(shape, dtype = float, order = 'C')

numpy.empty(shape, dtype = float, order = 'C')

где:

shape - обязательный аргумент, кортеж, требуемая размерность массива;

dtype - опциональный аргумент, тип элементов массива, по умолчанию float;

order - опциональный аргумент, строка, способ представления данных массива в памяти, два возможных значения 'C' и 'F', пока я не сталкивался с необходимостью изменять умолчальное значение.

Ну и последний из рассматриваемых способов с помощью функций numpy.zeros_like(), numpy.ones_like(), numpy.empty_like().

Обязательный аргумент, принимаемый функциями - массив, функции возвращают массив такой же структуры, содержащий, соответственно, нули, единицы и то, что оказалось в памяти на момент создания массива.

>>> d
array([ 1.,  2.,  3.,  4.,  5.])

>>> dz = np.zeros_like(d)
>>> dz
array([ 0.,  0.,  0.,  0.,  0.])

>>> do = np.ones_like(d)
>>> do
array([ 1.,  1.,  1.,  1.,  1.])

>>> de = np.empty_like(d)
>>> de
array([  2.24122267e+201,   6.32526950e-317,   0.00000000e+000,
         2.24686637e+201,   6.34874355e-321])

Полный формат вызова функций:

numpy.zeros_like(a)

numpy.ones_like(a)

numpy.empty_like(a)

где:

a - обязательный аргумент, массив, структуру которого необходимо повторить;

О массивах чуть подробней

Как я уже говорил массив это упорядоченная "многомерная таблица" содержащая элементы одного типа, доступ к которым осуществляется по индексу. Индекс - кортеж целых чисел, однозначно определяющий положение элемента в массиве.

Многомерную таблицу можно представить как некое расширение обычной, "двумерной" таблицы, включающей кроме строк и столбцов еще произвольное число "измерений", вместе образующих некую многомерную решетку. В документации NumPy такие измерения именуют осями (axis), а число осей у конкретного массива рангом (rank) массива (при этом термин ранг применяется и в контексте матриц, что, разумеется, не одно и тоже). Для еще большей путаницы вместо числа осей или ранга используют термин размерность (dimension). В разделе документации официального сайта проекта есть Numpy Glossary, там для слова axis приводиться одно значение, для слова rank два, а для слова dimension - три. На текущем уровне просветления моё воображение позволяет представить массив с размерностью не большей четырех, а в практической деятельности, я не сталкивался с массивами имеющими более трех осей :) Так вектор это одномерный массив, матрица, растровый черно-белый рисунок, таблица Excel двумерный, цветной растровый рисунок трехмерный.

Каждый объект класса numpy.ndarray имеет атрибут ndarray.ndim - число осей, ранг, размерность массива. По определению ранга массива значение ndarray.ndim должно быть равно числу элементов в кортеже ndarray.shape.

Общее число элементов массива можно узнать, обратившись к атрибуту ndarray.size.

>>> import numpy as np

>>> vector = np.array([1, 3, 5, 7, 9])
>>> print vector.ndim
1
>>> print vector.shape
(5,)
>>> vector.size
5

>>> bwimage = np.array([ [255, 247, 236, 12, 149], [123, 34, 147, 45, 102], [34, 69, 108, 81, 94] ])
>>> print bwimage.ndim
2
>>> print bwimage.shape
(3, 5)
>>> bwimage.size
15

>>> rgbimage = np.array([ [ [234, 126, 34, 45, 18], [123, 123, 49, 34, 56], [255, 233, 233, 233, 233] ],
... [ [12, 12, 12, 12, 12], [14, 15, 16, 17, 17], [13, 12, 14, 12, 12] ],
... [ [67, 56, 56, 57, 56], [56, 57, 56, 57, 58], [59, 58, 58, 59, 57] ] ])
>>> print rgbimage.ndim
3
>>> print rgbimage.shape
(3, 3, 5)
>>> rgbimage.size
45

В принципе с размерностями и рангами можно особо не заморачиваться, рассматривая многомерные массивы как вложенные (массивы, содержащие другие массивы) при этом следует не забывать, что длинна всех массивов находящихся на одном уровне вложения (на одной оси) обязана быть одинаковой.

>>> good = np.array([ [1, 2, 3], [4, 5, 6], [7, 8, 9] ])
>>> wrong = np.array([ [1, 2, 3], [4, 5, 6], [7, 8] ])
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: setting an array element with a sequence.

Операции над массивами

Все вышесказанное было бы абсолютно бесполезной белибердой, если бы над массивами (над данными содержащимися в массивах) невозможно было б производить каких либо содержательных действий. Разумеется это не так. Цель создания пакета NumPy - предоставить пользователю Python инструменты для "быстрой" работы с большими наборами данных.

Объекты класса numpy.ndarray можно использовать как операнды в выражениях, при этом все операции с массивами будут выполняться поэлементно, то есть итогом операции будет новый массив, содержащий результаты применения операции к каждому элементу исходного массива:

>>> import numpy as np

>>> a = np.arange(6)
>>> print a
[0 1 2 3 4 5]

>>> print a + 1
[1 2 3 4 5 6]

>>> print a * 3
[ 0  3  6  9 12 15]

>>> print a ** 3
[  0   1   8  27  64 125]

>>> print a < 3
[ True  True  True False False False]

>>> a += 2
>>> print a
[2 3 4 5 6 7]

В пакете NumPy определены основные математические функции, так же позволяющие проводить поэлементные вычисления:

>>> t = np.linspace(0.0, 2 * np.pi, 4)
>>> print t
[ 0.          2.0943951   4.1887902   6.28318531]

>>> print np.cos(t)
[ 1.  -0.5 -0.5  1. ]

>>> print np.sin(t)
[  0.00000000e+00   8.66025404e-01  -8.66025404e-01  -2.44929360e-16]

>>> print np.tan(t)
[  0.00000000e+00  -1.73205081e+00   1.73205081e+00  -2.44929360e-16]

>>> s = np.linspace(2.0, 6.0, 5)
>>> print s
[ 2.  3.  4.  5.  6.]

>>> s = np.exp(s)
>>> print s
[   7.3890561    20.08553692   54.59815003  148.4131591   403.42879349]

>>> s = np.log(s)
>>> print s
[ 2.  3.  4.  5.  6.]

>>> print np.sqrt(s ** 2)
[ 2.  3.  4.  5.  6.]

Привожу список самых полезных (на мой взгляд) математических функций пакета NumPy:

Во всех определениях ниже a массив или скаляр.

numpy.abs(a) - абсолютное значение a;

numpy.around(a, decimals = 0, out = None) - округляет a до заданного количества десятичных разрядов, по умолчанию до целого. Придерживается следующего правила округления. Если значение a находиться точно по середине между двумя целыми, округление производиться до ближайшего четного целого. Так если a равно 1.5 или 2.5 будет возвращено 2, если a равно -0.5 или 0.5 будет возвращено 0.0. Аргумент decimals - целое, десятичный разряд после запятой, до которого производиться округление, если decimals отрицательное, разряд отсчитывается влево от запятой.

>>> print np.around(np.array([0.5, 1.8, 2.5, 3.5]))
[ 0.  2.  2.  4.]

>>> print np.around(np.array([1, 5, 15, 45]), decimals = 1)
[ 1  5 15 45]

>>> print np.around(np.array([1, 5, 15, 45]), decimals = -1)
[ 0  0 20 40]

Аргумент out - массив, в который будет передан результат, структура массива out, должна совпадать со структурой возвращаемого массива. Если None (по умолчанию) будет создан новый массив.

numpy.fix(a, out = None) - отбрасывает дробную часть a;

numpy.ceil(a, out = None) - округляет a до меньшего из целых больших или равных a;

>>>  print np.ceil(np.array([-2.7, -1.2, -0.5, 1.8, 2.4, 3.6]))
[-2. -1. -0.  2.  3.  4.]

numpy.floor(a, out = None) - округляет a до большего из целых меньших или равных a;

>>> print np.floor(np.array([-2.7, -1.2, -0.5, 1.8, 2.4, 3.6]))
[-3. -2. -1.  1.  2.  3.]

numpy.sign(a) - возвращает -1 если a < 0, 0 если a == 0, 1 если a > 0;

numpy.degrees(a) - конвертирует a из радиан в градусы;

numpy.radians(a) - конвертирует a из градусов в радианы;

numpy.cos(a), numpy.sin(a), numpy.tan(a) - возвращает косинус, синус, тангенс a. a в радианах;

numpy.cosh(a), numpy.sinh(a), numpy.tanh(a) - возвращает гиперболические косинус, синус, тангенс a. a в радианах;

numpy.arccos(a), numpy.arcsin(a), numpy.arctan(a) - возвращает арккосинус, арксинус, арктангенс a в радианах. Для арккосинуса в диапазоне [0, nump.pi], для арксинуса [-numpy.pi/2, numpy.pi/2], для арктангенса [-numpy.pi/2, numpy.pi/2];

numpy.arccosh(a), numpy.arcsinh(a), numpy.arctanh(a) - возвращает гиперболические косинус, синус, тангенс a. a в радианах;

numpy.exp(a) - возвращает основание натурального логарифма (число e) в степени a;

numpy.log(a), numpy.log10(a), numpy.log2(a) - возвращает натуральный логарифм a, логарифм a по основанию 10, логарифм a по основанию 2;

numpy.log1p(a) - возвращает натуральный логарифм a + 1;

numpy.sqrt(a) - возвращает положительный квадратный корень a;

numpy.square(a) - возвращает квадрат a.

В выражения можно включать несколько массивов. В случае если атрибуты ndarray.shape этих массивов совпадают, результат очевиден - действия над массивами будут производиться поэлементно:

>>> a1 = np.array([ [1.0, 2.0], [3.0, 4.0] ])
>>> a2 = np.array([ [5.0, 6.0], [7.0, 8.0] ])
>>> a3 = np.array([ [9.0, 10.0], [11.0, 12.0] ])

>>> print a1 + a2 + a3
[[ 15.  18.]
 [ 21.  24.]]

>>> print a1 * a2
[[  5.  12.]
 [ 21.  32.]]

>>> print a3 / a1
[[ 9.          5.        ]
 [ 3.66666667  3.        ]]

>>> print (a3 - a1) * a2
[[ 40.  48.]
 [ 56.  64.]]

Если атрибуты ndarray.shape не совпадают - действия над массивами производятся в соответствии с концепцией транслирования (broadcasting).

Операция транслирования - расширение одного или обоих массивов операндов до массивов с равной размерностью.

Для начала несколько примеров:

>>> a2 = np.array([1, 2])
>>> print a2
[1 2]
>>> print a2.shape
(2,)

>>> a22 = np.array([ [1, 2], [3, 4] ])
>>> print a22
[[1 2]
 [3 4]]
>>> print a22.shape
(2, 2)

>>> a32 = np.array([ [1, 2], [3, 4], [5, 6] ])
>>> print a32
[[1 2]
 [3 4]
 [5 6]]
>>> print a32.shape
(3, 2)

>>> a222 = np.array([ [ [1, 2], [3, 4] ], [ [5, 6], [7, 8] ] ])
>>> print a222
[[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]]
>>> print a222.shape
(2, 2, 2)

>>> print a22 + a2
[[2 4]
 [4 6]]
 
>>> print a32 + a2
[[2 4]
 [4 6]
 [6 8]]

>>> print a222 + a2
[[[ 2  4]
  [ 4  6]]

 [[ 6  8]
  [ 8 10]]]

>>> print a32 + a22
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: shape mismatch: objects cannot be broadcast to a single shape

>>> print a222 + a22
[[[ 2  4]
  [ 6  8]]

 [[ 6  8]
  [10 12]]]

>>> print a222 + a32
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: shape mismatch: objects cannot be broadcast to a single shape

И так правило. Если длины осей массивов, начиная с замыкающей, попарно равны или в каждой из сравниваемых пар длин хотя бы одна равна единице, то к таким массивам может быть применена операция транслирования. Вот. Длина замыкающей оси - длина массива вложенного наиболее глубоко.

>>> a = np.ones((7, 3, 4, 9, 8))
>>> b = np.ones((4, 9, 8))
>>> c = np.ones((4, 3, 8))

>>> print (a + b).shape
(7, 3, 4, 9, 8)

>>> print (a + c).shape
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: shape mismatch: objects cannot be broadcast to a single shape

>>> d = np.ones((9, 7, 1, 6, 1))
>>> e = np.ones((7, 2, 1, 4))
>>> print (d + e).shape
(9, 7, 2, 6, 4)

В случае если в массивах присутствуют оси единичной длины, расширяться могут оба массива.

>>> f = np.array([1, 2])
>>> print f
[1 2]
>>> print f.shape
(2,)

>>> g = np.array([ [3], [4], [5] ])
>>> print g
[[3]
 [4]
 [5]]
>>> print g.shape
(3, 1)

>>> h = f + g
>>> print h
[[4 5]
 [5 6]
 [6 7]]
>>> print h.shape
(3, 2)

Трансляция массивов происходит и при вызове некоторых функций.

Например, функция numpy.power(a1, a2), где a1, a2 массив или скаляр, возвращает a1 в степени a2:

>>> print np.power(np.array([-2.0, -1.0, 0.0, 2.0, 3.0, 4.0]), 4)
[  16.    1.    0.   16.   81.  256.]

>>> print np.power(np.array([-2.0, -1.0, 0.0, 2.0, 3.0, 4.0]), -4)
[ 0.0625      1.                 Inf  0.0625      0.01234568  0.00390625]

в случае если у переданных массивов не совпадает структура, проводит трансляцию.

>>> print np.power(np.array([3, 7]), np.array([ [1], [2], [3] ]))
[[  3   7]
 [  9  49]
 [ 27 343]]

Некоторые полезные функции

Здесь я приведу еще один набор полезных функций.

numpy.min(a, axis = None, out = None),

numpy.max(a, axis = None, out = None) -

возвращает минимальное, максимальное значение элементов массива соответственно:

>>> import numpy as np

>>> print np.min(np.array([ [1.0, -0.5, 3.0], [4.0, 3.0, -0.5] ]))
-0.5

axis - опциональный аргумент, индекс оси (измерения) массива по которому проводится поиск минимального, максимального значения. Под индексом оси понимается индекс в кортеже ndarray.shape.

>>> a = np.array([ [ [1.0, 2.0, 3.0], [4.0, 5.0, 6.0] ], [ [7.0, 8.0, 9.0], [11, 12, 13] ] ])
>>> print a
[[[  1.   2.   3.]
  [  4.   5.   6.]]

 [[  7.   8.   9.]
  [ 11.  12.  13.]]]
>>> print a.shape
(2, 2, 3)

>>> print np.min(a, axis = 0)
[[ 1.  2.  3.]
 [ 4.  5.  6.]]

>>> print np.min(a, axis = 1)
[[ 1.  2.  3.]
 [ 7.  8.  9.]]

>>> print np.min(a, axis = 2)
[[  1.   4.]
 [  7.  11.]]

out - опциональный аргумент, массив, в который будет помещен результат. Структура массива out должна соответствовать структуре массива результата. Если out = None (по умолчанию) будет создан новый массив.

numpy.argmin(a, axis = None),

numpy.argmax(a, axis = None) -

возвращает индекс минимального, максимального значения элементов массива соответственно:

>>> print np.argmin(np.array([ [1.0, -0.5, 3.0], [4.0, 3.0, -0.5] ]))
1

>>> print np.argmin(a, axis = 0)
[[0 0 0]
 [0 0 0]]

>>> print np.argmin(a, axis = 1)
[[0 0 0]
 [0 0 0]]

>>> print np.argmin(a, axis = 2)
[[0 0]
 [0 0]]

numpy.sum(a, axis = None, dtype = None, out = None),

numpy.prod(a, axis = None, dtype = None, out = None) -

возвращает сумму, произведение элементов массива соответственно:

>>> print np.sum(np.array([ [1.0, -0.5, 3.0], [4.0, 3.0, -0.5] ]))
10.0
>>> print np.sum(a, axis = 0)
[[  8.  10.  12.]
 [ 15.  17.  19.]]
>>> print np.sum(a, axis = 1)
[[  5.   7.   9.]
 [ 18.  20.  22.]]
>>> print np.sum(a, axis = 2)
[[  6.  15.]
 [ 24.  36.]]

Ну вот пожалуй на сегодня и все. Разговор о пакете NumPy продолжим в следующий раз.

Читать далее...